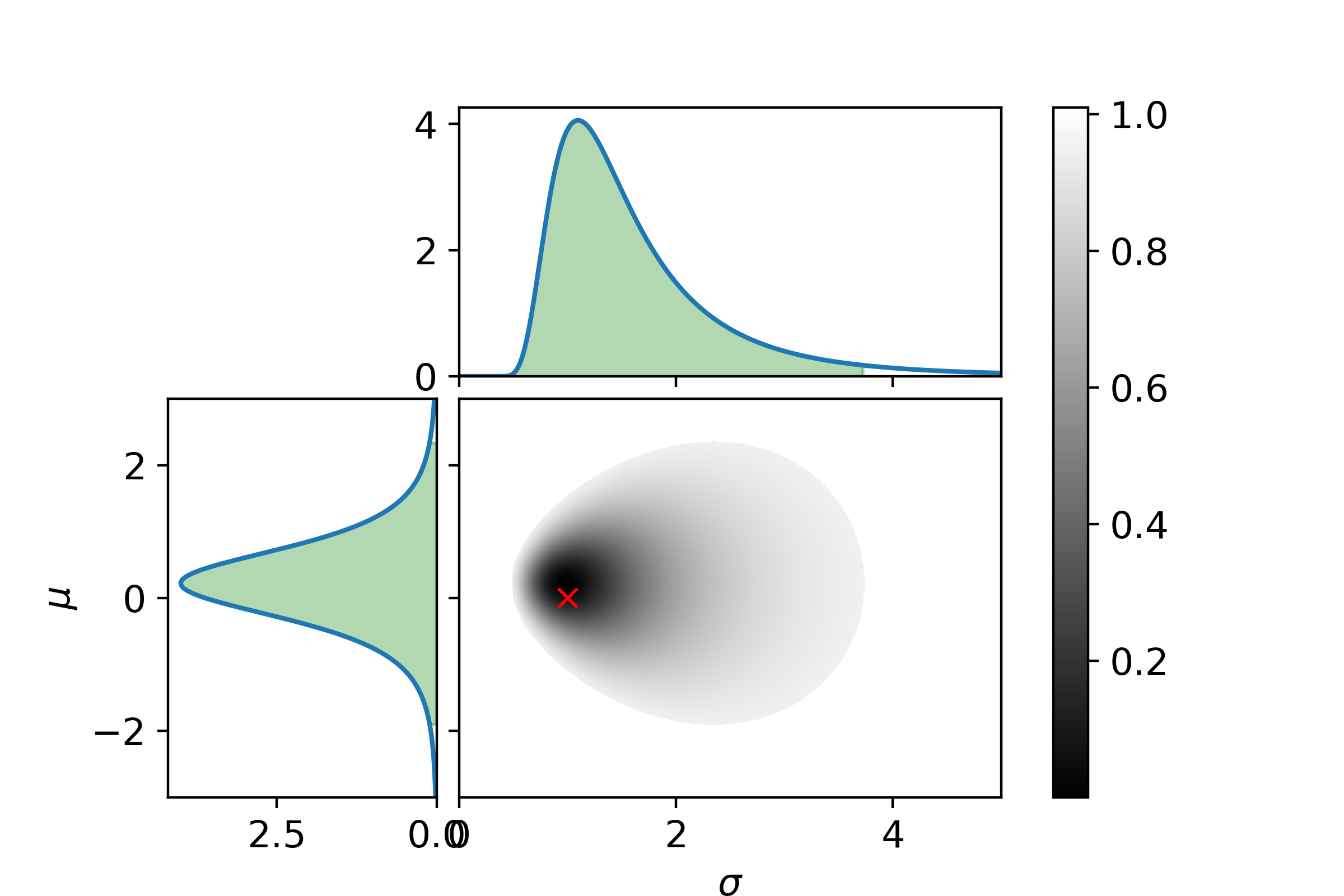
In a previous post Bayesian interference was used to parameter likelyhood of a binomial distribution. The binomial distribution can be used to describe events with discrete probabilities. However, a lot of interesting probabilistic events are continuous. One of the most...
The content creator Matt Parker made a YouTube video titled Can you find: five five-letter words with twenty-five unique letters?. The essence of the question at hand is how many combinations of five five-letter words exist such that all twenty-five...
In many games, different items or events have an associated chance to appear. Often these chances are unknown to the players. In this post, we will try to estimate the chance of getting a Mysterious Stranger in Hearthstone Mercenaries from...
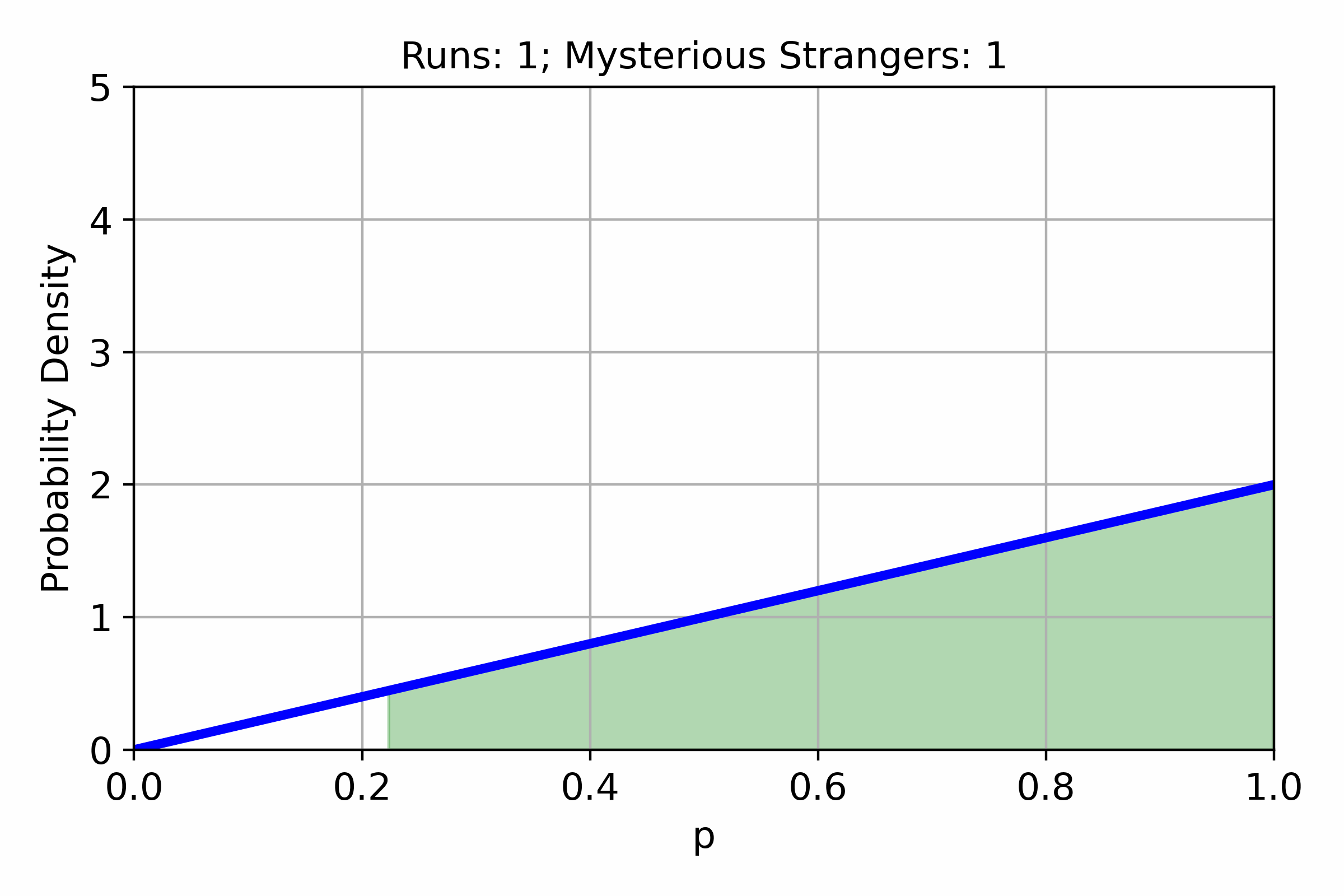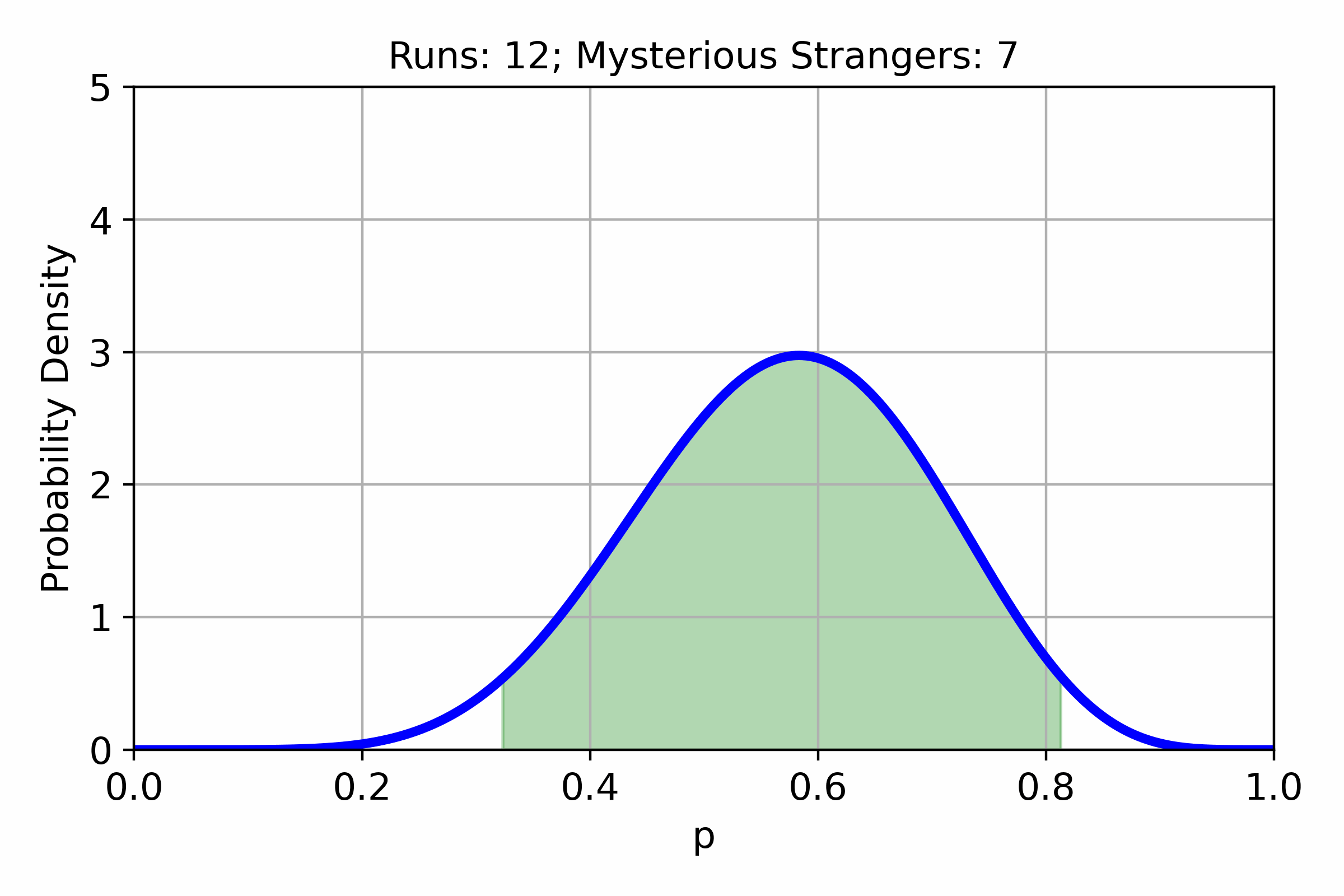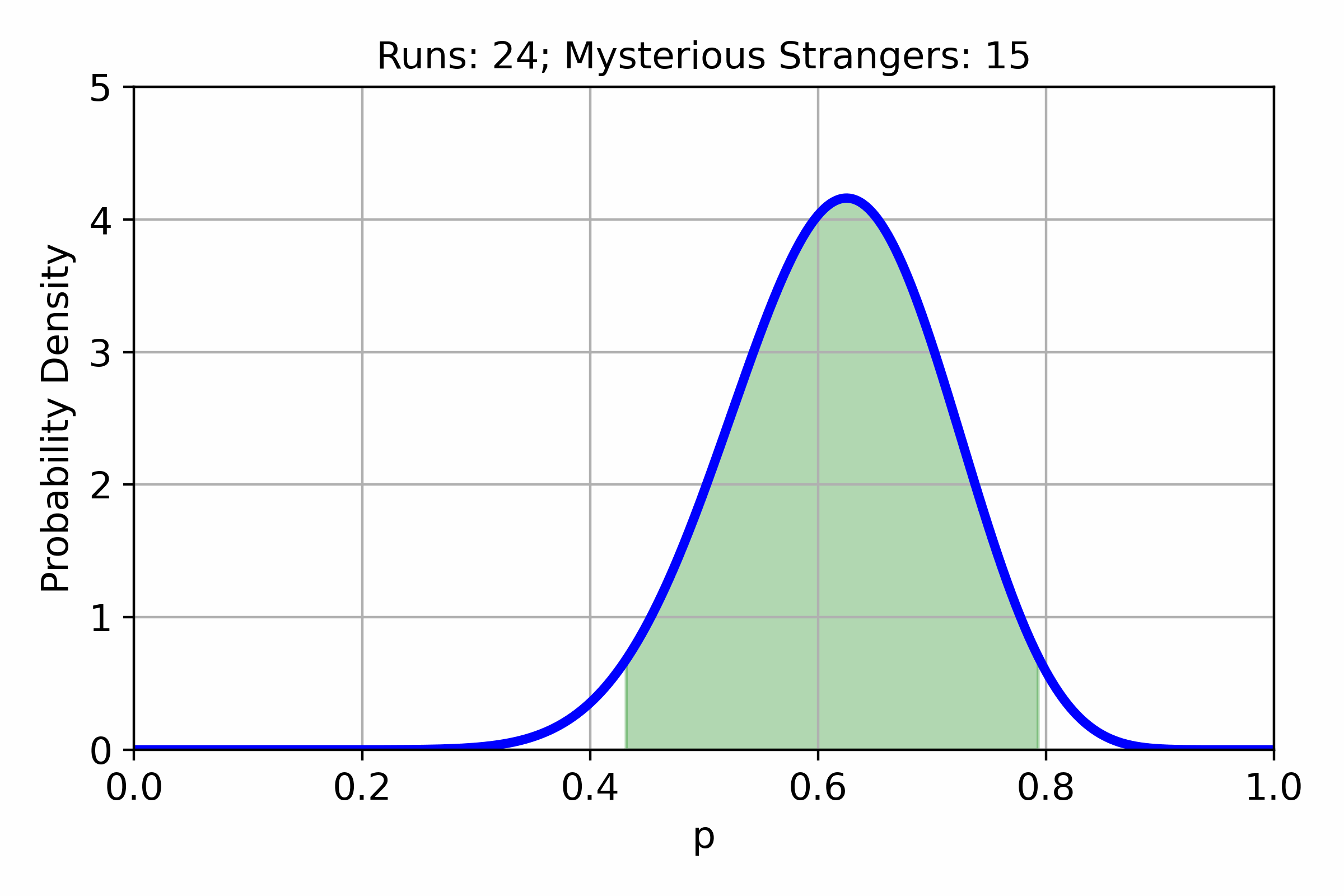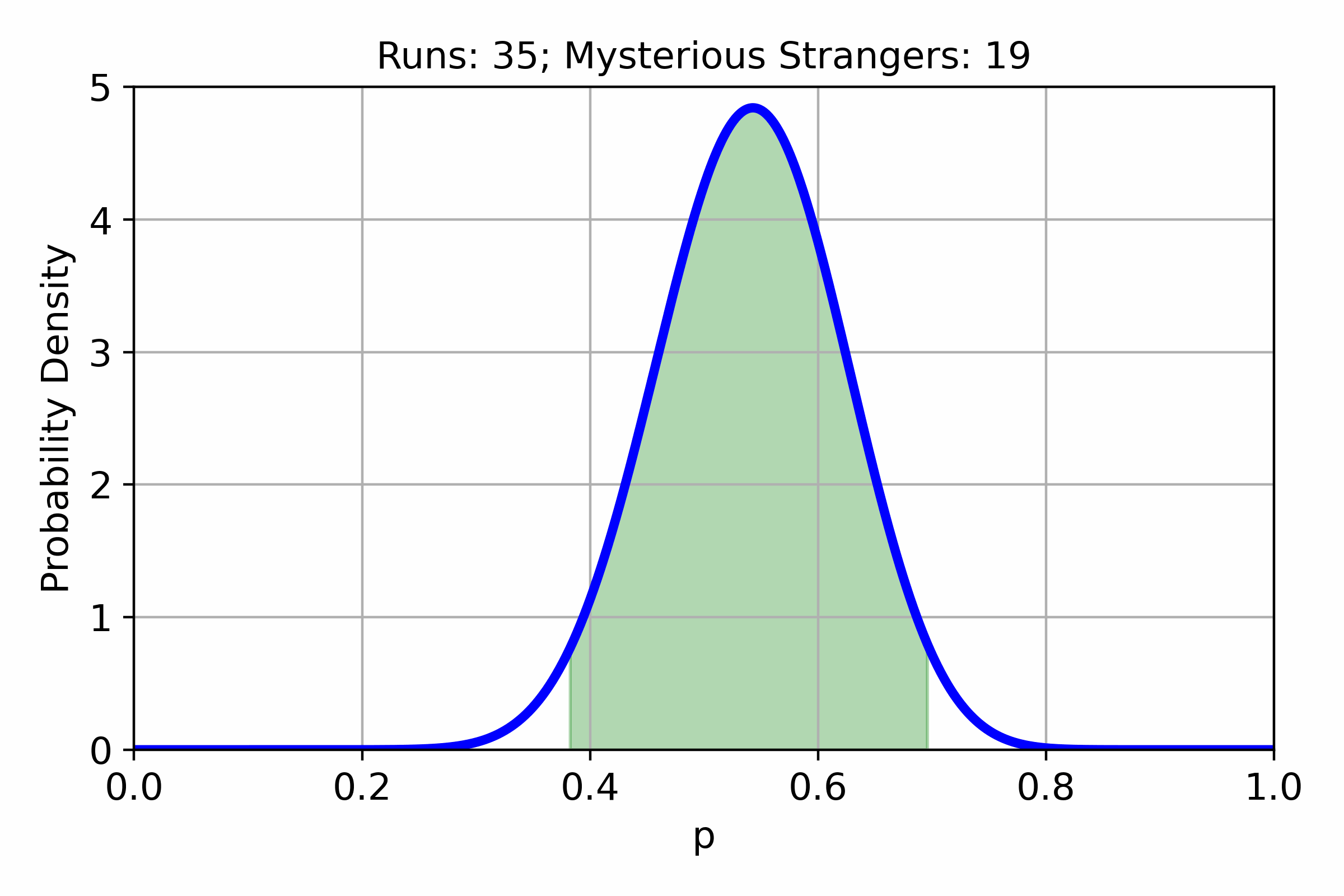
In Hearthstone battlegrounds as of patch 18.6.1 the Amalgadon card have the following effect: Battlecry: For each different minion type you have among other minions, Adapt randomly. When playing Amalgadon the number of adapts will be in the range between...

Consider a function: \[f\left(x_{1}\left(\lambda_{1},\lambda_{2},..,\lambda_{M}\right),x_{2}\left(\lambda_{1},\lambda_{2},..,\lambda_{M}\right),..,x_{N}\left(\lambda_{1},\lambda_{2},..,\lambda_{M}\right)\right)\] The first partial derivative is given as: \[\frac{\partial}{\partial\lambda_{i}}f\left(x_{1},x_{2},..,x_{N}\right)=\frac{\partial f}{\partial x_{1}}\frac{\partial x_{1}}{\partial\lambda_{i}}+\frac{\partial f}{\partial x_{2}}\frac{\partial x_{2}}{\partial\lambda_{i}}+...+\frac{\partial f}{\partial x_{N}}\frac{\partial x_{N}}{\partial\lambda_{i}}\] The above equation can be formulated as: \[\frac{\partial}{\partial\lambda_{i}}f\left(x_{1},x_{2},..,x_{N}\right)=\sum_{k}^{N}\frac{\partial f}{\partial x_{k}}\frac{\partial x_{k}}{\partial\lambda_{i}}\] Now consider the second derivative: \[\frac{\partial^{2}}{\partial\lambda_{j}\partial\lambda_{i}}f\left(x_{1},x_{2},..,x_{N}\right)=\frac{\partial}{\partial\lambda_{j}}\left(\frac{\partial f}{\partial x_{1}}\frac{\partial...

