This post is inspired by a paper by Ali Alavi and a talk by Frank Neese at ICQC 2023. The goal of the work by Frank Neese and Ali Alavi is to be able to describe a wave function with...

In the decision of which funds to invest in, an important parameter is how well the fund can track the benchmark index. It is to be expected that the variance of how well a specific fund can track an index...
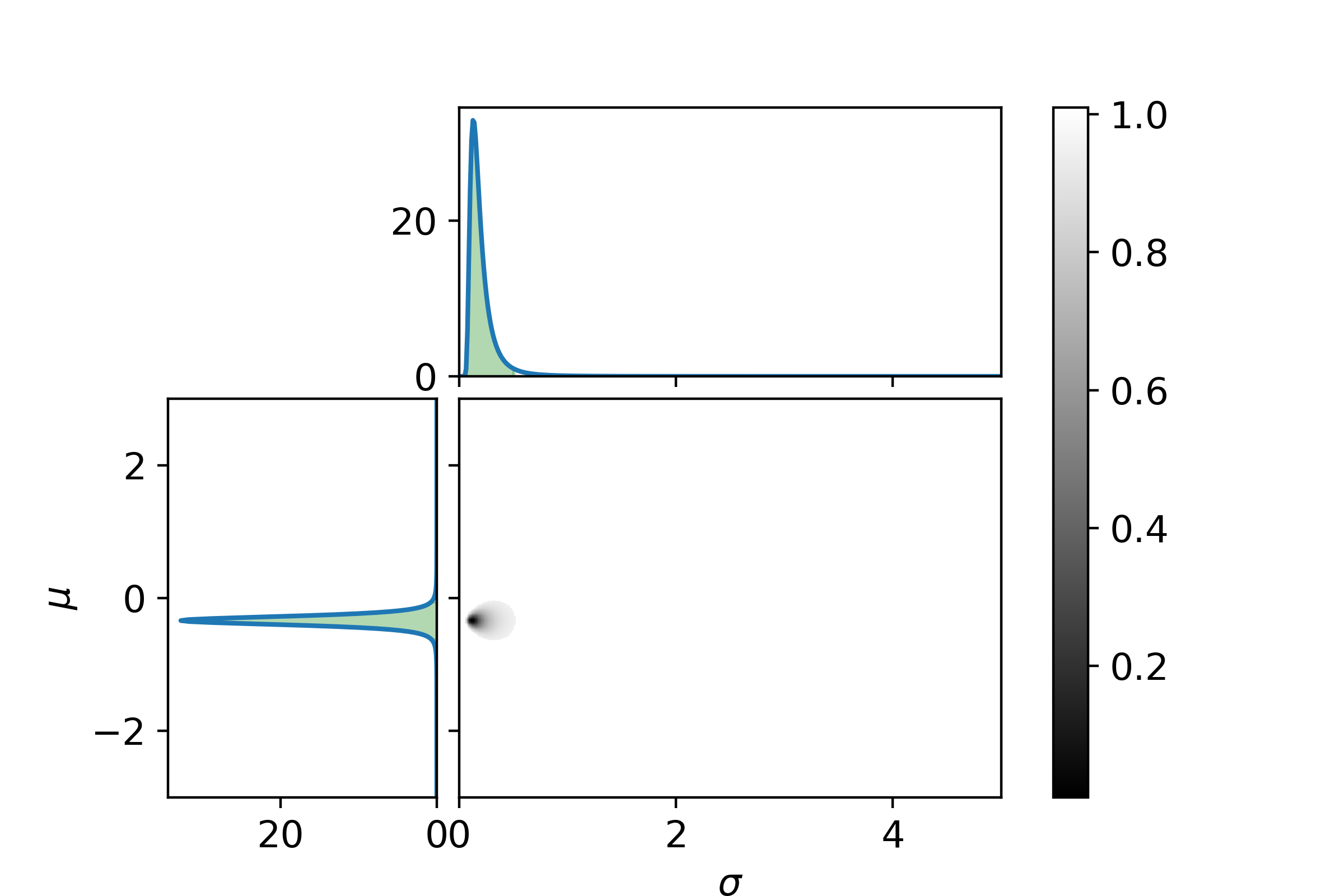
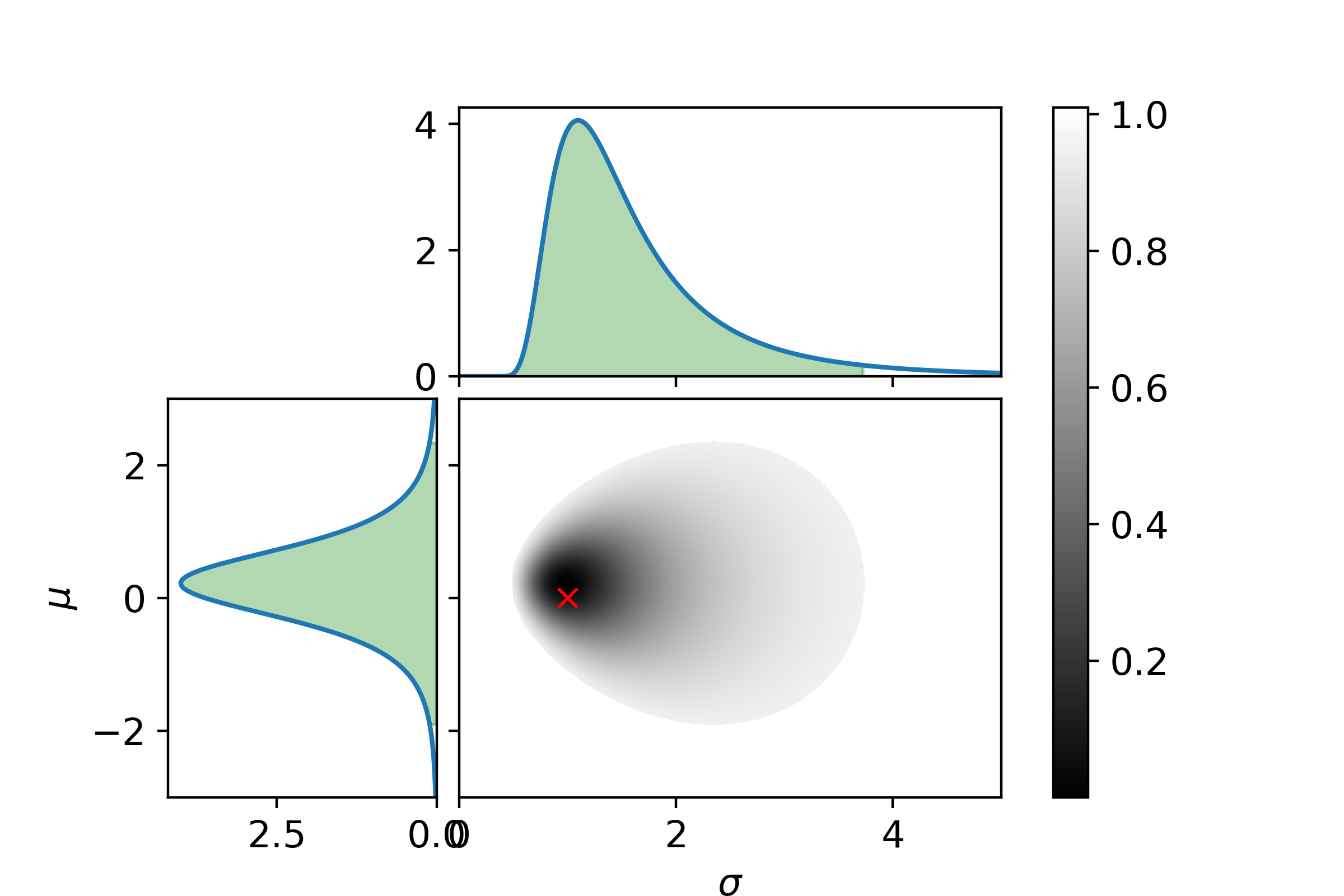
In a previous post Bayesian interference was used to parameter likelyhood of a binomial distribution. The binomial distribution can be used to describe events with discrete probabilities. However, a lot of interesting probabilistic events are continuous. One of the most...
In a previous post the Jordan-Wigner representation of the molecular Hamiltonian for the hydrogen molecule was constructed. This Hamiltonian was solved explicit diagonalization. The method of explicit diagonalization quickly becomes computationally impossible when the dimension of the Hamiltonian grow, and...
The first step of using quantum computers to perform quantum chemical simulations is to translate the fermionic Hamiltonian to a qubit Hamiltonian (represented by Pauli operators). The fermionic Hamiltonian in spin basis is: \[H = \sum_{pq}h_{pq}a^\dagger_p a_q + \frac{1}{2}\sum_{pqrs}g_{pqrs}a^\dagger_p a^\dagger_q...
The hydrogen molecule in a minimal basis (STO-3G as an example) will have a full CI Hamiltonian that is only four by four (using determinants that are singlet). The four determintants in second quantization langauge are \(\left|1100\right>\), \(\left|1001\right>\), \(\left|0110\right>\), and,...
In a previous post the Hellmann-Feynman forces where calculated using PySCF, and used gradient descent to optimize the geometry of the molecule. Geometry optimization is however a surprising hard problem to do, and writing algorithms from scratch might result in...
The Hellmann-Feynman theorem states that: \[\frac{\mathrm{d}E}{\mathrm{d\lambda}} = \left<\psi\left|\frac{\mathrm{d}\hat{H}}{\mathrm{d}\lambda}\right|\psi\right>\] It should be noted that for a finite basis this theorem does not hold, and might want to account for Pulay forces. For the molecular Hamiltonian: \[\hat{H} = -\frac{1}{2}\sum_i\nabla_i^2 - \sum_{iK}\frac{Z_K}{r_{iK}} +...

Current quantum computers work with unitary gates. In order to represent operators relevant for quantum chemistry on a quantum computer, unitary operators are thus needed. The condition for a unitary operator is: \[UU^\dagger = I\] It can easily be checked...
Coming from a theoretical chemistry background, I have mostly learned second quantization from Molecular Electronic-Structure Theory. From here the algebra is taught with the ON vector, \(\left|10\right>\) denoting the first orbital being occupied and the second orbital being unoccupied. In...
The content creator Matt Parker made a YouTube video titled Can you find: five five-letter words with twenty-five unique letters?. The essence of the question at hand is how many combinations of five five-letter words exist such that all twenty-five...
In the United Kingdom investors can invest in a class of bonds known as premium bonds. Premium bonds does not have a fixed coupon-rate, but yield is instead distributed via. lottery. The prizes distributed as of May 2022 are: Prize...

Over the past 25 years the house prices have appreciated by a factor of ~3.5. But what drivers have been the primiary for this prise appreciation, and can this continue going forward? The primiary drivers for appreciation of house prices...

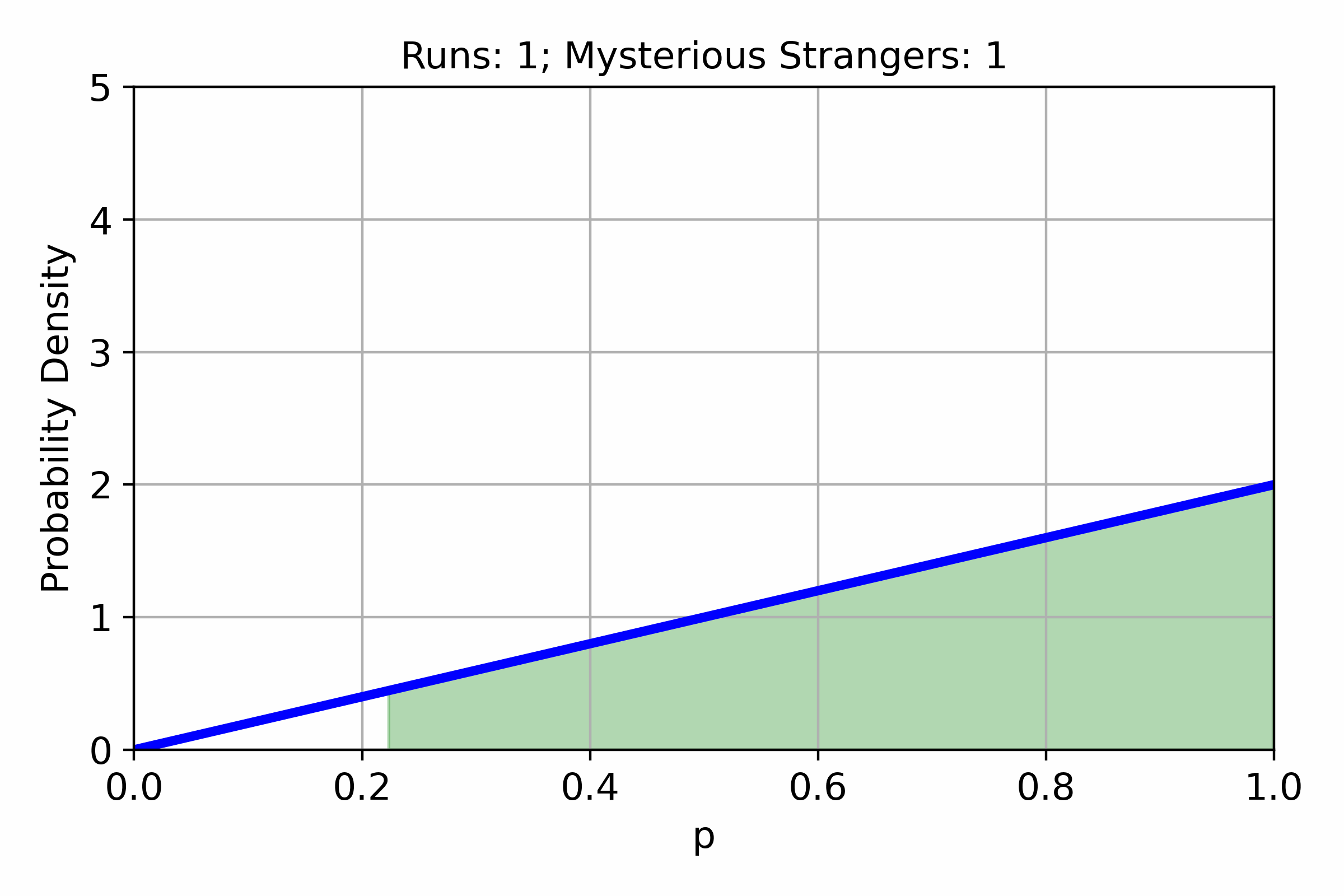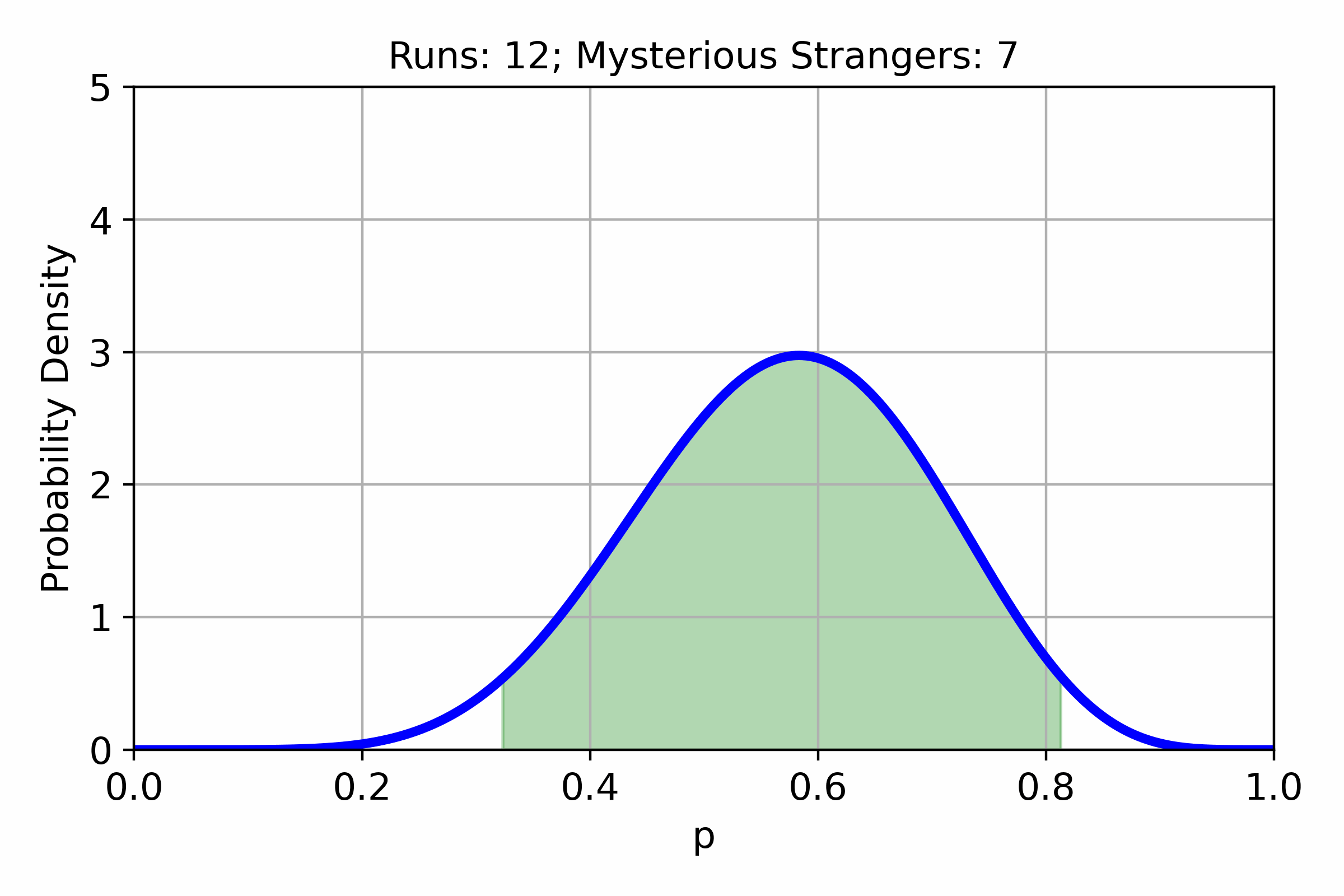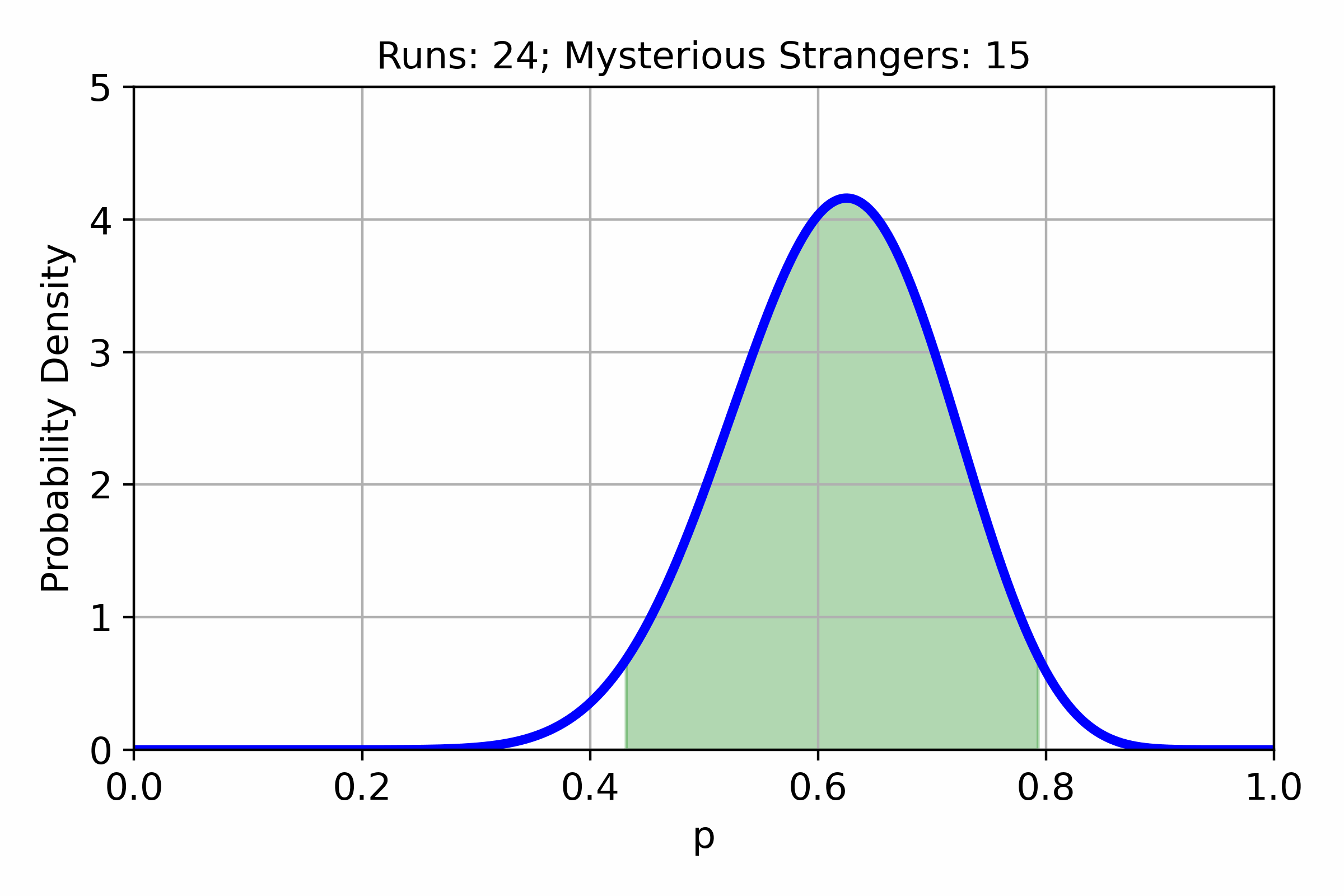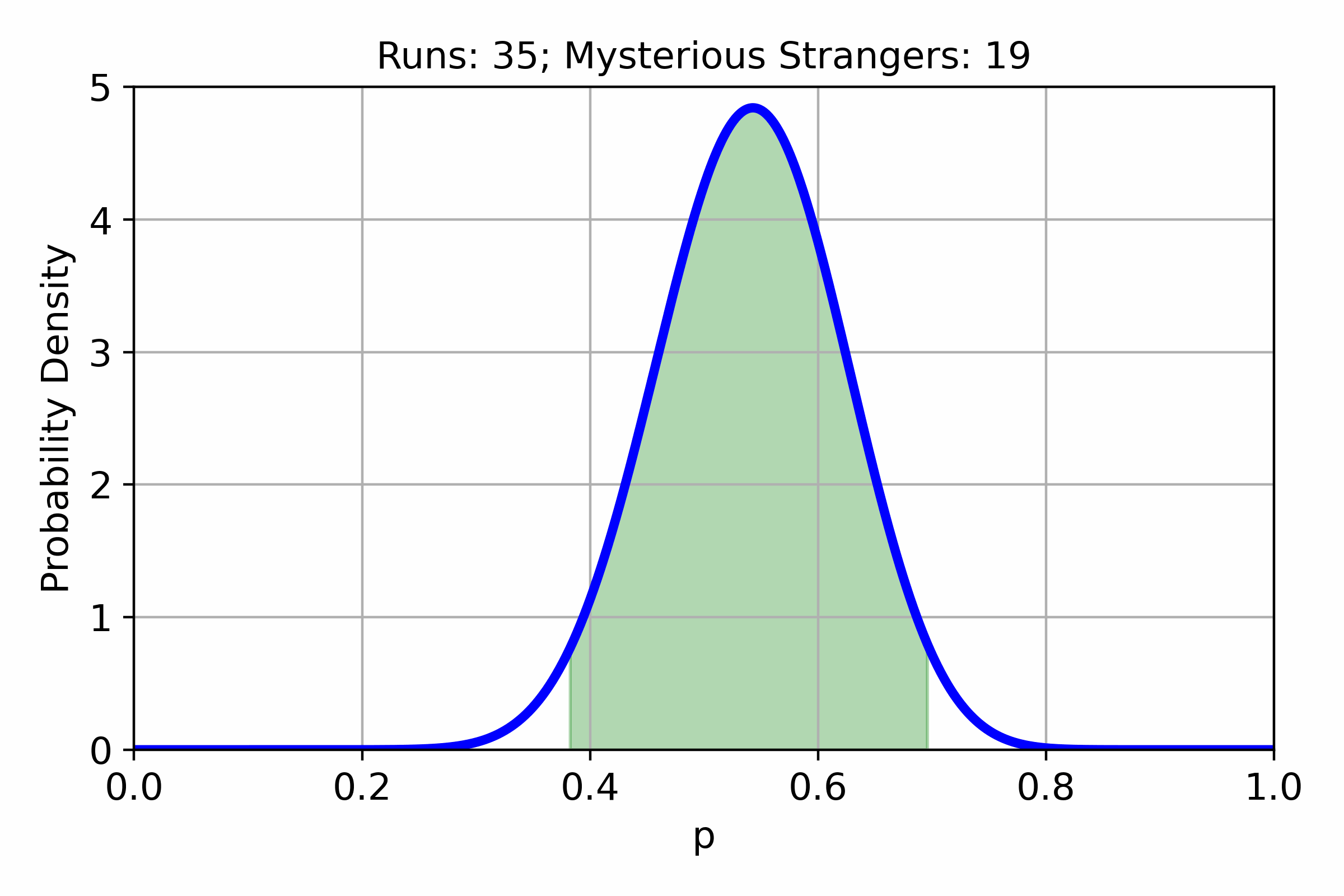
In many games, different items or events have an associated chance to appear. Often these chances are unknown to the players. In this post, we will try to estimate the chance of getting a Mysterious Stranger in Hearthstone Mercenaries from...
In Hearthstone battlegrounds as of patch 18.6.1 the Amalgadon card have the following effect: Battlecry: For each different minion type you have among other minions, Adapt randomly. When playing Amalgadon the number of adapts will be in the range between...

Given the selection of Danish investment funds from Sparindex and Danske Invest, it can be difficult to see how different the funds are. As a measure of similarity, one can calculate the overlap between two funds. The overlap between fund...

In Denmark, all ETFs are taxed yearly by unrealized returns. On the other hand, some Danish investment funds are taxed by realized gain, if they fulfill some criteria of paid out dividends. The dividend paid out will be: earned dividends...

Many brokers (at least in Denmark), have a pricing model of \(q\%\) of the trading amount or minimum \(q\) Euro. Given a fixed amount to invest every month, we might think it is best to accumulate the cash to reach...

Following the source: A. Rizzo, S. Coriani, and K. Ruud, Computational Strategies for Spectroscopy. From Small Molecules to Nano Systems, edited by V. Barone (John Wiley and Sons, 2012) Chap. 2, pp.77–135. It is given in Eq. (2.35) that: \[\varepsilon(\omega)...
In quantum chemstry integrals of the following form are sometimes needed: \[F_a = \left<\phi_i\left|\nabla^a r^{-1}\right|\phi_j\right>\] But these integrals are often not directly available. What instead is available is integrals of the form: \[f_a = \left<\nabla^a\phi_i\left|r^{-1}\right|\phi_j\right>\] \[f_{a,b} = \left<\nabla^a\phi_i\left|r^{-1}\right|\nabla^b\phi_j\right>\] Let us...
Consider the electrostatic potential due to multipoles places at the position of atoms: \[E_{i}=\sum_{j}^{atom}\sum_{n}^{multipole}\frac{\left(-1\right)^{n}}{n!}T_{ij}^{(n)}m_{j}^{(n)}\] If the quantum mechanical electrostatic potential is to be minimized, a cost function can written of the form: \[z=\sum_{i}^{point}\left(V_{i,\mathrm{QM}}-E_{i}\right)^{2}+\sum_{l}^{constraints}\lambda_{l}g_{l}\] Expanding the square: \[z=\sum_{i}^{point}\left(V_{i,\mathrm{QM}}^{2}+E_{i}^{2}-2E_{i}V_{i,\mathrm{QM}}\right)+\sum_{l}^{constraints}\lambda_{l}g_{l}\] It is known...
Consider a function: \[f\left(x_{1}\left(\lambda_{1},\lambda_{2},..,\lambda_{M}\right),x_{2}\left(\lambda_{1},\lambda_{2},..,\lambda_{M}\right),..,x_{N}\left(\lambda_{1},\lambda_{2},..,\lambda_{M}\right)\right)\] The first partial derivative is given as: \[\frac{\partial}{\partial\lambda_{i}}f\left(x_{1},x_{2},..,x_{N}\right)=\frac{\partial f}{\partial x_{1}}\frac{\partial x_{1}}{\partial\lambda_{i}}+\frac{\partial f}{\partial x_{2}}\frac{\partial x_{2}}{\partial\lambda_{i}}+...+\frac{\partial f}{\partial x_{N}}\frac{\partial x_{N}}{\partial\lambda_{i}}\] The above equation can be formulated as: \[\frac{\partial}{\partial\lambda_{i}}f\left(x_{1},x_{2},..,x_{N}\right)=\sum_{k}^{N}\frac{\partial f}{\partial x_{k}}\frac{\partial x_{k}}{\partial\lambda_{i}}\] Now consider the second derivative: \[\frac{\partial^{2}}{\partial\lambda_{j}\partial\lambda_{i}}f\left(x_{1},x_{2},..,x_{N}\right)=\frac{\partial}{\partial\lambda_{j}}\left(\frac{\partial f}{\partial x_{1}}\frac{\partial...


